Serie n. 7 - Gioco n. 024

i disegni del nipotino

Durante l'Estate il mio nipotino Antonio si è divertito a disegnare alcune locomotive che, per un verso o per l'altro, si somigliavano tutte. Alla vista di quei disegnini mi son venuti in mente quei quiz attitudinali presenti in molti manuali di giochi dei quali ne propongo uno al gentile navigatore.

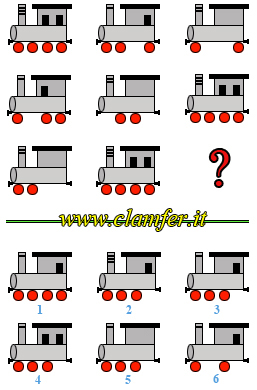
Nella prima parte della tavola che segue sono riportati 8 disegni di locotender, sistemati da sinistra verso desta e dall'alto in basso, secondo una certa logica.

Sapreste indicare quale delle 6 locotender disegnate nella seconda parte della tavola deve essere inserita al posto del punto interrogativo?

SOLUZIONE

Serie n. 7 - Gioco n. 025

Questo non è il solito giochino, ma una magia operata dal famoso Mago Merlino, quel mago che, dopo tanti prodigi, qualche tempo addietro si diede agli spot televisivi dopo aver inventato nientepocodimeno che: l'acqua calda.

Rinsavito dopo questa breve esperienza, ha voluto proporci una sua magia per assistere alla quale devi cliccare con il mouse sulla scritta sopra il tram.

Ad ogni click seguirà una nuova scritta. Buon divertimento!

SOLUZIONE

Rubrica ideata e curata da Antonio Gamboni

SERIE 7: Soluzioni dei Giochi

Soluzione Serie n. 7 - Gioco n. 022

quattro amici a tavola

La soluzione è molto semplice. Supponiamo di voler disporre i quattro amici su una sola sedia; si hanno quattro possibilità, cioè D(4,1) = 4. Se però le sedie sono due, possiamo assegnare il primo posto in quattro modi possibili mentre per il secondo si dovrà scegliere fra i tre amici rimasti e cioè D(4,2) = 4x(4-1).

Ripetendo il ragionamento fino a considerare tutte le quattro sedie, avremo:

D(4,4) = 4x(4-1)x(4-2)x(4-3) = 24

Si tratta in realtà di calcolare le permutazioni di quattro oggetti su quattro posti.

Tornando al quesito, la prima posizione sarà ripetuta dopo 12 giorni in quanto per ogni giorno vi sono due diverse disposizioni: l'una a pranzo e l'altra a cena.

Ma poiché il viaggio dura solo 67 ore, pari a circa 3 giorni, se ne deduce che Maurice, Jeannot, Margot e Geneviéve non riusciranno ad esaurire tutti i possibili modi di sedere a tavola.

TORNA AL GIOCO

Soluzione Serie n. 7 - Gioco n. 023

una famiglia numerosa

Per arrivare alla soluzione, si cominci con l'osservare che il resto OO è minore del divisore SEM il che vuol dire che la seconda cifra E del quoziente è zero. Ciò ci consente di affermare che il prodotto M x M, ovvero il quadrato di M, è uguale ad RO. D'altra parte si ha L - O = O, ossia L è il doppio di O, quindi O è uguale a 4 o è minore di 4. Allora il quadrato di M, che dovrà essere un numero di 2 cifre in quanto uguale a RO, potrà finire per 1 o per 4, così che M potrà essere 9 oppure 8.

Nel caso in cui M = 8, sarebbe uguale ad L = 2 x O = 2 x 4. tale ipotesi è da escludersi dovendo essere tutte le lettere espresse da cifre diverse.

Quindi M = 9 e, di conseguenza, O = 1, L = 2 e R = 8.

La divisione a questo punto assume l'aspetto:

Da tale operazione si rileva che CA rappresenta il prodotto 9 x S. Poiché S, C ed A devono avere valori diversi dalle cifre finora trovate, esse dovranno scegliersi tra i numeri 3, 4, 5, 6 e 7.

Ora se S fosse 5, anche A sarebbe 5. Nel caso S = 3, C sarebbe uguale a 2, ovvero uguale ad L. Dunque S dovrà essere 4, 6 oppure 7.

Ricordando che Carluccio non paga il biglietto, C non potrà essere 6 e neppure 7; quindi C o è 3 o è 4.

Ed ancora, se S fosse 6, si avrebbe C = 5, in contrasto con quanto precedentemente affermato; se invece fosse S = 7, si avrebbe C = 6 (da escludersi per lo stesso motivo). Quindi S non può essere che 4. Da ciò ne segue che C = 3 ed A = 6; pertanto l'operazione ricostruita sarà:

TORNA AL GIOCO

Soluzione Serie n. 7 - Gioco n. 024

i disegni del nipotino

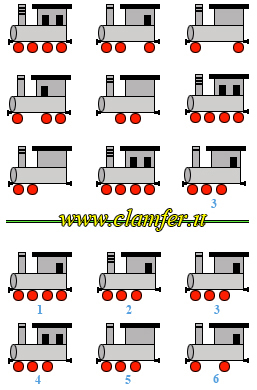
Cominciamo con l'osservare che gli elementi che caratterizzano i diversi disegni sono solo tre: il numero di ruote (2, 3, 4), le righe sul fumaiolo (1, 2, 3) ed il numero dei finestrini (0, 1, 2).

Ruote:

avendosi in ciascuna riga ed in ciascuna colonna una locomotiva con due ruote, una con tre ed un'altra con quattro, la loco mancante dovrà avere tre ruote; pertanto sarà la 2, 3, 4 o 5.

Fumaiolo:

anche in questo caso in ciascuna riga ed in ciascuna colonna vi sono locotender con fumaioli aventi una riga, due righe e tre righe. Poiché manca il fumaiolo con una riga, dai numeri 2, 3, 4 e 5 prima selezionati si scarterà la n. 2.

Finestrini:

stesso discorso per i finestrini. Dovendo avere la locomotiva mancante un solo finestrino, la soluzione è data dalla locotender n. 3.

TORNA AL GIOCO

Soluzione Serie n. 7 - Gioco n. 025

la magia di Mago Merlino

Siamo spiacenti per non poter dare la soluzione causa mancata comunicazione della stessa da parte di Mago Merlino!

TORNA AL GIOCO